Ordinal Inscriptions & Fears of Clogging The Blockchain
Inscriptions aren't the fabled DDoS attack on bitcoin. The Bitcoin network and its endgame as a global financial settlement layer are unaffected.
Dear readers,
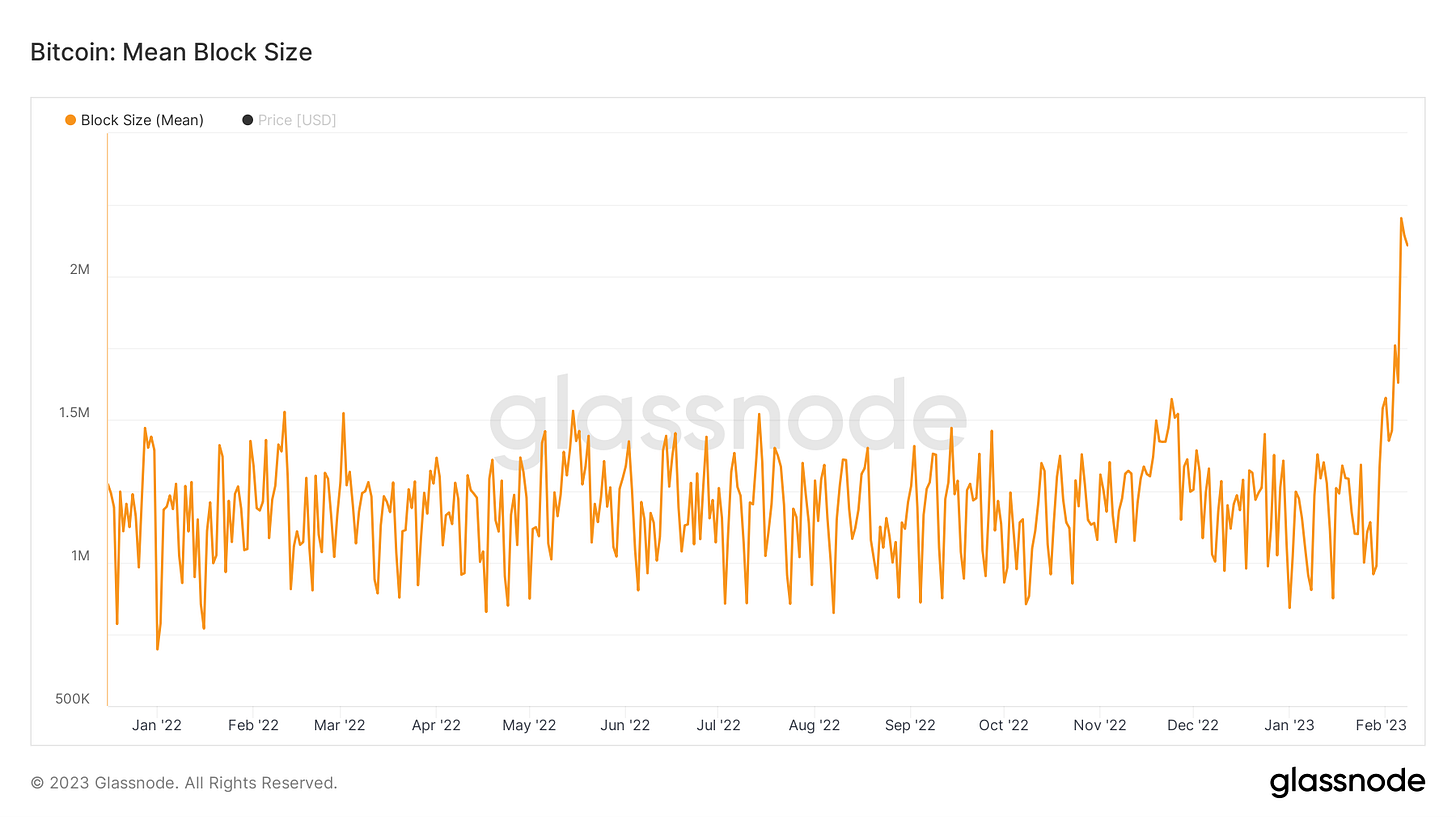
Last week, the Bitcoin protocol was altered forever when a 3.96-megabyte block was hashed onto the blockchain at block height 774628. The reason for this unusually large block is one that gives most longtime bitcoin proponents pause: a .jpeg image. The opining about bitcoin’s end-of-days are misplaced, however. As the Bitcoin protocol grows into a global financial settlement layer over the next several decades, valuable and increasingly expensive block space makes any attempt at bloating the blockchain with still images a seriously expensive form of attacking Bitcoin.
Ordinals are a numerical labeling scheme for individual satoshis. Using these unique labels as identifiers, arbitrary data like still images can be “attached” to satoshis. Just as they do for any other transaction to be added onto bitcoin’s blockchain, users creating these inscriptions must pay a fee commensurate to the size of the asset they’re storing. The average size of a bitcoin block has risen past 2 megabytes in the wake of ordinal inscriptions becoming more widely used:
These ordinal labels are externally projected onto the satoshis, and not directly on bitcoin’s base layer. This is an important distinction; if they were an alteration to Bitcoin Core and directly visible with any regular full node, bitcoin’s fungibility may be inexorably damaged. Transacting bitcoin would be made exceedingly more difficult as different satoshis would have different values, and the interchangeability, one BTC equalling one BTC, would be threatened. Thankfully, this is not the case; Bitcoin Core is not aware of inscriptions. Ordinal labeling and inscriptions don’t damage bitcoin’s fungibility because it’s an opt-in convention; you don’t have to observe them if you don’t want to. You can transact bitcoin regularly without witnessing or even acknowledging ordinal numbers on individual sats—let’s explain why.